Introducción #
Ejemplo extraído del video Machine Learning episodio 5. Estimador de incertidumbre. Se pondrán imagens obtenidas del video para explicar mejor el funcionamiento tal como lo hace en el video.
El ejemplo esta creado el Jupiter Notebool y se irá poniendo el código de las distintas celdas
El estimador de incertidumbre es una función que viene incluida en algunos algoritmos de Scikit learn(Sklearn), y nos ayuda a ver como de seguro esta nuestro algoritmo al clasificar un nuevo valor o punto, como lo llama en el video. El estimador es el paquete SVM dentro de la librería de Sklearn.
Ejemplo si tenemos un algoritmo que tiene que clasificar entre 0 y 1, el estimador nos va a decir que tan seguro se siente nuestro algoritmo para predicir que el nuevo valor lo va a clasificar al grupo 0 o al grupo 1. Por ejemplo nos puede servir para detectar que si un nuevo punto el algorito nos dice que esta al 50% seguro que lo va a clasificar al grupo 0, podríamos llegar a la conclusión que preferimos que no haga la predicción. Porque podría ser igual de valido que se clasificará al grupo 1. Ya que el nuevo valor tiene las misma posibilidades de ir a un grupo como al otro.
El uso del SVM es útil para poder escoger el algoritmo que nos va mejor a la hora de clasificar. Lo que hay que tener en cuenta el sobreajuste, si un algoritmo esta muy seguro a la hora de clasificar puede ser que este sobreajustando por lo tanto habrá que tratar dicho ajuste.
Codigo #
El primer paso es siempre cargar las librerías.
# Set de datos
from sklearn.datasets import load_iris
# Separador de datos de entrenamiento y test
from sklearn.model_selection import train_test_split
# Libreria de los estados de incertidumbre
from sklearn import svm
Datos para las pruebas
# Carga del modelo de datos
iris=load_iris()
Generación de las variables con los datos
X_ent, X_test, y_ent, y_test = train_test_split(iris.data, iris.target)
Variable para poder poner en marcha el SVM
# Se crea la variable con el algoritmo SVM
algoritmo = svm.SVC(probability=True)
Paso habitual para entrenar el algoritmo
# Entrenamiento del algoritmo
algoritmo.fit(X_ent, y_ent)
Se informo como se quiere que se comporte el SVM.
algoritmo.decision_function_shape = "ovr"
# decision_function nos va a devolver un numero que nos va a decir que
# tan lejos esta el punto del hiperplano que clasifica.
# Al algoritmo se le pasa los valores de testing y que solo nos traiga 10 ejemplos.
algoritmo.decision_function(X_test)[:10]
En este trozo de código vamos a explicar como funciona el SVM tal como lo hace el video. Veamos el siguiente modelo de datos:
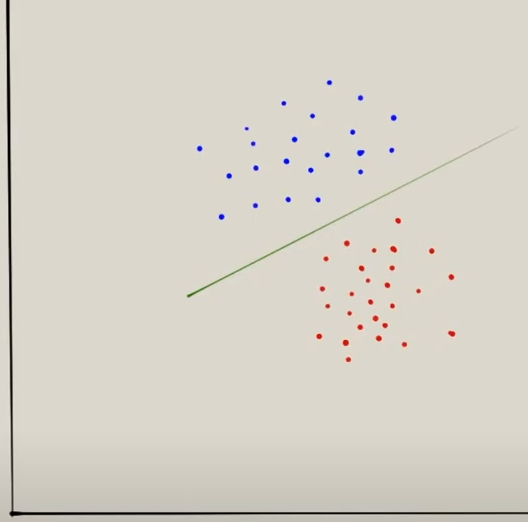
La línea verde o hiperplano nos separa los puntos azules de los rojos. Lo que queremos que devuelva el algoritmo sea el número más alto, ya que indicará que esta lo más alejado posible de la línea/hiperplano. Si el algoritmo un número que esta sobre la línea no va a estar muy seguro de como clasificarlo, pero si el punto esta lo más lejano de la línea el algoritmo va a estar más seguro a la hora de clasificarlo.
El resultado que devuelve al ejecutar es el siguiente:
array([[-0.20269857, 2.23688486, 0.84169686],
[-0.21313057, 2.23268086, 0.88330921],
[ 2.22580348, 1.15214418, -0.24872264],
[ 2.23455235, 1.13095515, -0.25044655],
[ 2.23313006, 1.13211798, -0.24964792],
[ 2.2269661 , 1.1259788 , -0.24423893],
[-0.23439994, 1.08865842, 2.22247787],
[-0.23387148, 1.18608119, 2.17366629],
[ 2.22684708, 1.14267576, -0.24739233],
[-0.21427536, 2.21884877, 0.96646885]])
Que significa, que el primer registro o dato lo va a clasificar en el segundo grupo porque es el número más alto, es decir, el más alejado al hiperplano. En el segundo datos también iría al segundo grupo, pero en el tercer dato lo clasificaría en el primer grupo.
NOTA: Nos devuelve tres grupos la función porque en el set de datos de Iris soy hay tres tipos de flores para clasificar
Se lanza otra función contra los datos de test para devuelve unos valores similares al código anterior pero a nivel de probalidad.
# Esta función nos va decir algo parecido al "decision_function" pero en el
# ámbito de la probabilidad.
# Se le pasa los datos de testing y se le indica que solo procese los 10 primeros
algoritmo.predict_proba(X_test)[:10]
El resultado que devuelve al ejecutar es el siguiente:
array([[0.01701662, 0.97626968, 0.0067137 ],
[0.01130569, 0.97524721, 0.0134471 ],
[0.95145127, 0.03609592, 0.01245281],
[0.97121252, 0.01879533, 0.00999214],
[0.96865943, 0.02079702, 0.01054356],
[0.95443207, 0.03348436, 0.01208357],
[0.00997134, 0.04291861, 0.94711005],
[0.01111241, 0.46790436, 0.52098323],
[0.95385933, 0.03421938, 0.0119213 ],
[0.01653293, 0.95084668, 0.03262039]])
Aquí vemos que el primer dato lo va clasificar al segundo grupo con un 97% de probabilidades, lo mismo para el segundo datos. Pero para el tercer registro iría al primer grupo con un 95% de probabilidades.
Como se ve la clasificación es coherente con la función anterior.
NOTA: La suma de los porcentajes de cada fila va ser del 100%
Finalmente se lanza la función de predicción para ver como va a predecir el algoritmo.
# Con al función o algoritmo predict nos va a decir como va a predecir el algoritmo de clasificación
algoritmo.predict(X_test)[:10]
El resultado que devuelve al ejecutar es el siguiente:
array([1, 1, 0, 0, 0, 0, 2, 2, 0, 1])
El resultado que devuelve coincide con los valores que nos han devuelto las funciones anteriores. Hay que recordar que los arrays empiezan por el índice 0, por lo tanto en el primer registro que vale “1” equivale al 97% que devuelve el PREDICT_PROBA y el “2.23” que devuelve la función DECISION_FUNCTION