Introducción #
Ejemplo extraído del video Machine Learning episodio 10. Procesamiento de datos (PCA). De este mismo video se extraerán fotos para aclarar mejor conceptos tal como hace el video.
El ejemplo esta creado el Jupiter Notebool y se irá poniendo el código de las distintas celdas.
Explicación #
La librería PCA se utiliza para principalmente dos cosas:
- Reducir el ruido que hay en nuestros datos
- Poder ver los datos que están en muchas dimensiones en solo dos dimensiones. En muchos set de datos hay treinta características distintas que a nivel gráfico es muy complicado de ver y entender. Con PCA permite reducir las treinta dimensiones en tal solo dos lo que permite ver correlaciones que nos pueda interesar o entender mejor la información.
Para enteder como funciona el algoritmo partimos de la siguiente imagen:
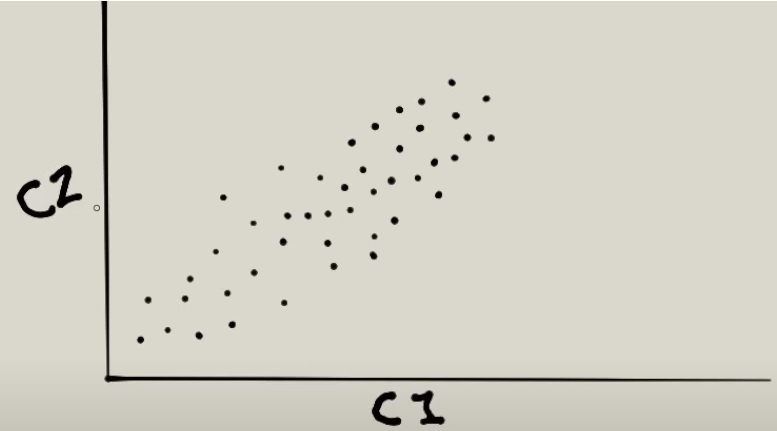
Tenemos dos ejes que representan dos características. Lo primero que va hacer detectar PCA es en que dirección hay más variedad de datos que sería la siguiente:
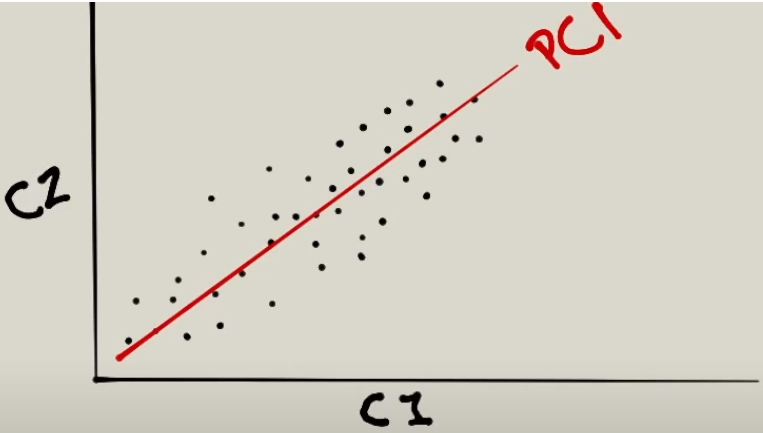
Esta primera línea la llama Principal component 1(PCA1). Lo siguiente que va hacer es encontrar un eje ortoganal, es decir a 90º grados, el cual intentar maximizar la variedad de datos que sería el que se ve en la siguiente imagen en color verde:
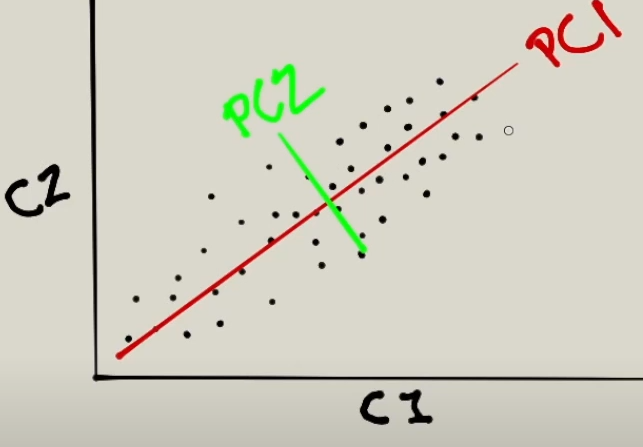
Este nueva dirección la va a llamar PCA2. Lo siguiente que hará PCA es tomar estos dos ejes como nuevos parámetros para poderlos mostrar gráficamente todos los puntos que existen. De esta manera va a poder hacer una representación abstracta de nuestros datos.
Código #
import sklearn
# Librería para representar gráficamente los datos
import mglearn
# Datos sobre el cancer donde tiene 30 características para
# saber si un tumor es maligno o benigno
from sklearn.datasets import load_breast_cancer
# Librería para la representación gráfica
import matplotlib.pyplot as plt
# Algoritmo PCA
from sklearn.decomposition import PCA
# Permite ver las gráficas en nuestro editor jupyter
%matplotlib inline
# Ejemplo de lo que hace PCA
# En el recuadro "original data" se ve como encuentra los dos ejes
# explicados anteriormente. El largo es el component 1 y el corto el 2
# Aquí se ve mejor el eje ortogonal
# En el recuadro "transformed data" lo que hace es ver los datos horizontalmente
# lo que hace es retar el valor promedio a cada datos haciendo que los datos
# se centren en el eje 0.
# En el recuadro "transformed data..." lo que hace es representar los datos
# con el eje horizontal del component 1. El segundo eje va ser las caracaterísticas
# (feature 2) de la primera gráfica. Lo que se ve es una línea recta de los datos
# que se ven la segunda gráfica al eje del component 1.
# En el recuadro "back-rotation..." lo que hace es sumar de nuevo el promedio
# que le resto en la segunda gráfica y lo va rotar de nuevo. Con lo cual
# queda como en la primera imagen pero eliminando el ruido que habia.
mglearn.plots.plot_pca_illustration()
Imagen con la imagen que devuelve el ejemplo:
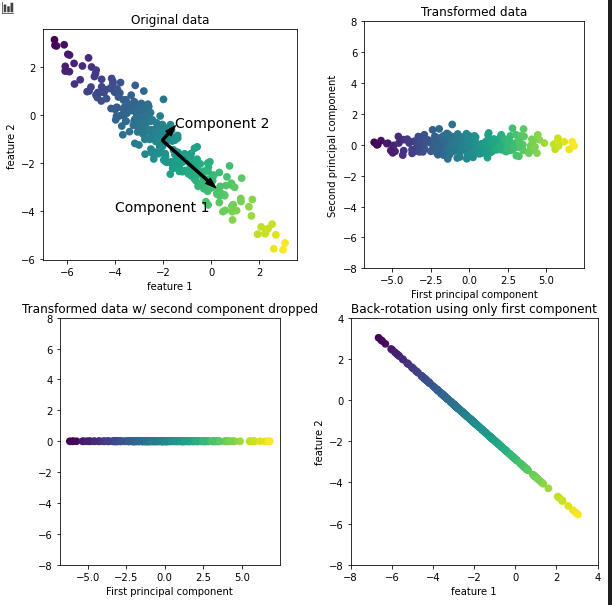
# Datos para entrenar el algoritmo
cancer = load_breast_cancer()
print("Valor de las características: ", cancer.feature_names)
print("Número de características: ", cancer.feature_names.shape)
# Algoritmo PCA donde se le indica el número de ejes.
# El eje 1 será el que más variedad de datos talc omo se ve en el gráfico
# de ejemplo. El eje 2 que es el ortogonal.
pca = PCA(n_components=2)
# Datos para el entrenamiento algoritmo
pca.fit(cancer.data)
# Genera una variable con los datos transformados.
# Es decir, transforma las 30 características a las 2 que se
# le ha indicado
transformada = pca.transform(cancer.data)
# Comparativa de las características originales versus la transformada
print("Mediciones, características de los datos originales: ", cancer.data.shape)
print("Mediciones, características de los datos procesados: ", transformada.shape)
# Al gráfico se le pasa como eje X los valores principal, y en el 1 las características
mglearn.discrete_scatter(transformada[:,0],transformada[:,1], cancer.target)
plt.legend(cancer.target_names,loc='best')
plt.xlabel("PCA 1")
plt.ylabel("PCA 2")
El gráfico que aparecerá será el siguiente:
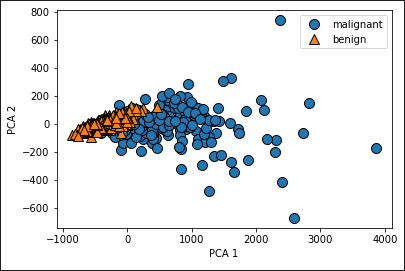
Este gráfico es una abstracción de los datos. En el se puede ver un comportamiento en los datos. Los triangulos narajanjas son tumores benignos y están agrupados en el lado izquierdo. Los triangulos azules son los tumores malignos y están agrupados en el lado derecho pero más dispersos algunos puntos.
# Para ver cuan de importante es procesar los datos y para ver
# se va usar la función MinMaxScaler que permitira ver los datos en una escalar similar,
# que será un rango de 0 a 1. De esta manera se puede validar que no se procesando datos
# con valores muy pequeños contra valores muy grandes.
from sklearn.preprocessing import MinMaxScaler
escala = MinMaxScaler()
# Pasamos los datos a la función
escala.fit(cancer.data)
# transformamos los datos para que todos los datos esten en rango similar, de 0 a 1.
escalada = escala.transform(cancer.data)
# Se le pasa los datos tratados al algoritmo PCA
pca.fit(escalada)
transformada=pca.transform(escalada)
mglearn.discrete_scatter(transformada[:,0],transformada[:,1], cancer.target)
plt.legend(cancer.target_names,loc='best')
plt.gca()
plt.xlabel("PCA 1")
plt.ylabel("PCA 2")
El resultado del gráfico es el siguiente:
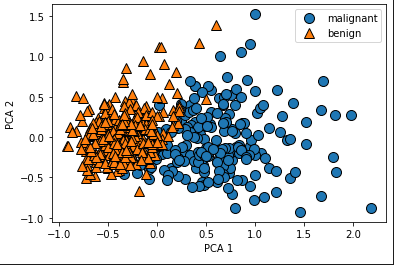
En este gráfico vemos que el rango del eje Y y X se han reducido respecto a los datos originales. Aquí también se puede ver que hay una correlación donde los tumores benignos están hacía la izquierda y los malignos a la derecha. Con lo cual los datos van a servir para hacer predicciones. A partir de aquí se puede decidir si el algoritmo lo entrenamos con la data real o con la transformada. Ya que si le enviamos los datos tratados claramente el algoritmo va trazar una línea que separe los datos de la izquierda y derecha para tratar los valores.
Finalmente dos sentencias para ver los datos tratados versus los datos sin tratar.
# Los datos escalados se verán que van siempre de 0 a 1.
print("Ejemplo de datos escalados: ", escalada)
# Aquí los datos son más dispersos lo que puede afectar al tratamiento en los algoritmos de clasificación
print("Ejemplo de datos sin escalar: ", cancer.data)