#import tensorflow as tf
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior() 
from tensorflow.examples.tutorials.mnist import input_data

mnist=input_data.read_data_sets("MNIST_data/", one_hot=True) #La imagenes tienen dimension de 28x28

x=tf.placeholder(tf.float32,[None,784]) #imagen del numero descompuesta a un vector
P=tf.Variable(tf.zeros([784,10])) #Matriz de pesos, 784 para recibir la imagen, 10 por las posible salidas
b=tf.Variable(tf.zeros([10])) #Vector con bias
y=tf.matmul(x,P)+b #La operacion que se hara en los nodos que reciben entradas
yR=tf.placeholder(tf.float32,[None,10]) # Matriz con las etiquetas REALES del set de datos

softmax=tf.nn.softmax_cross_entropy_with_logits(labels=yR,logits=y)
costo=tf.reduce_mean(softmax)
optimizador=tf.train.GradientDescentOptimizer(0.5).minimize(costo)

prediccion = tf.equal(tf.argmax(y, 1), tf.argmax(yR, 1)) #Nos da arreglo de booleanos para decirnos 
                                                         #cuales estan bien y cuales no
accuracy = tf.reduce_mean(tf.cast(prediccion, tf.float32))#Nos da el porcentaje sobre el arreglo de prediccion
Produccion = tf.argmax(y,1)
init=tf.global_variables_initializer()

#Funcion que usaremos para ver que tan bien va a aprendiendo nuestro modelo 
def avance(epoca_i, sess, last_features, last_labels):
    costoActual = sess.run(costo,feed_dict={x: last_features, yR: last_labels})
    Certeza = sess.run(accuracy,feed_dict={x:mnist.validation.images,yR: mnist.validation.labels})
    print('Epoca: {:<4} - Costo: {:<8.3} Certeza: {:<5.3}'.format(epoca_i,costoActual,Certeza))

with tf.Session() as sess:
    sess.run(init)
    for epoca_i in range(100):
        lotex, lotey = mnist.train.next_batch(100)
        sess.run(optimizador, feed_dict={x: lotex, yR: lotey})        
        if (epoca_i%50==0):
            avance(epoca_i, sess, lotex, lotey)
    print('RESULTADO FINAL: ',sess.run(accuracy, feed_dict={x: mnist.test.images,yR: mnist.test.labels}))
    print ('Resultado de una imagen',sess.run(Produccion,feed_dict={x: mnist.test.images[5].reshape(1,784)}))

mnist.test.labels[5]

#import tensorflow as tf
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior() 
from tensorflow.examples.tutorials.mnist import input_data

# Libreria tensor flowe
import tensorflow as tf
# Daset de datos con números escritos a manorom 
from tensorflow.examples.tutorials.mnist import input_data
import tensorflow_datasets as tfds
# API de tensorfow para construir y entrenar modelos de alto nivel
from tensorflow import keras
from keras.utils.np_utils import to_categorical

# Se recuperan los datos y el metadata de los datos
#mnist_train2, mnist_info = tfds.load('mnist', split='train', as_supervised=True,  shuffle_files=True,with_info=True)
# De los datos, se extrae los datos de entrenamiento y test
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(x_train.shape[0], 784)
x_test = x_test.reshape(x_test.shape[0], 784)

# El formato original esta en "unit8" con lo que se tiene que convertir en un float32 para que funcione
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')

#Se divide la imagen en 255 porque es la escala de grises y es mejor operar con 0 y 1. Más sencillo
x_train, x_test = x_train / 255.0, x_test / 255.0

# Paso necesario porque devuelve los registros y toda la información en la misma columna. Pero 
# se necesita esos valores esten en un matriz de 10 columnas para calcular bien los acietros.
y_train = to_categorical(y_train, 10)
y_test = to_categorical(y_test, 10)

mnist_train = tf.data.Dataset.from_tensor_slices((x_train, y_train))

# El ejemplo de .map es lo mismo que se ha hecho arriba cuando se han leido todos los datos
# El TFDS devuelve las imagenes en uint8, mientras que la red espera float 32
# hay que normalizar para que funcione
#def normalize_img(image, label):
#  """Normalizes images: `uint8` -> `float32`."""
#  return tf.cast(image, tf.float32) / 255, label
#
# map permite realizar una transformación a cada uno de los datos del conjuntos de datos
# que lo compone. En este caso lo que se se hace convertir las imagenes del TDFS al formato
# compatible de la red.
#mnist_train = mnist_train.map(
#    normalize_img, num_parallel_calls=tf.data.experimental.AUTOTUNE)
# Activa que los datos se guarden cache para mejorar el rendimiento
mnist_train = mnist_train.cache()
# Activa que los datos se recuperan de manera aleatoria
#mnist_train = mnist_train.shuffle(mnist_info.splits['train'].num_examples)
# Número de lotes que hará en cada iteracción
mnist_train = mnist_train.batch(100)

# Imagen del número descompuesto a un vector. Se informa que el vector es de 784 porque es
# multiplicación de 28 x 28 que son los pixeles de la imagen
# El valor None es para indicar que el valor, o filas, son variables según el número de imagenes
x = tf.keras.Input(name='x', shape=(None,784), dtype=tf.float32) 
# Matriz de pesos, que se inicializa a 0, con el tf.zeros. 
# La matriz tiene 784 filas, que son el número de pixeles. Y 10 columnas porque
# la siguienet capa tiene 10 elementos. La siguiente capa es la de salida
P = tf.Variable(tf.zeros([784,10]))
# Son los bias, o sesgo. Será un vector de 10 elementos inicializado a 0.
b = tf.Variable(tf.zeros([10]))
# Es la operación de salida. Aquí es la formula que se explica en la parte de redes
# neuronales, como funciona. 
# la formula es la multiplicación de la matriz de entrada * peso, más el sesgo.
y = tf.matmul(x,P)+b
# Matriz con las etiquetas reales del set de datos. Que tendrá un nuevo variable de filas
# y 10 columnas.
yR = tf.keras.Input(name='yR', shape=(None,10), dtype=tf.float32) 

print("x ", x.shape)
print("P ", P.shape)
print("b ", b.shape)

print("yr ", yR.shape)
print("y ", y.shape)

def compute_loss():
    log_x = tf.math.log(x)
    m = tf.math.square(log_x)
    return m

# Funcion para ver como esta aprendiendo el algoritmo
def avance(epoca_i,X_data, Y_data):
    x = X_data
    yR = Y_data
          
    y = tf.matmul(X_data,P)+b    

    #print("x ", x.shape)
    #print("P ", P.shape)
    #print("b ", b.shape)

    #print("yr ", Y_data.shape)
    #print("y ", y.shape)

    # Se definen los algoritmos de como va aprender la red en cada una de las iteracciones
    # Softmax nos va dar un vector de 10 elementos para generar la predicción pero en probabilidades
    # Esto nos va a dar un vector donde en cada posición nos va dar el % de probalidades que sea.
    # Es la libreria es la que nos va dar el error de nuestra predicciones. Se le pasará las 
    # etiquetas de los números y la salida de la red para que nos diga que tan bien o tan mal esta
    # el algoritmo para repartir los pesos.
    softmax = tf.nn.softmax_cross_entropy_with_logits(labels=Y_data,logits=y)
    
    # Es la función del coste de la predicción este número tiene que tender a 0.
    costo = tf.reduce_mean(softmax)
    
    # Código original tf.train.GradientDescentOptimizer(0.5).minimize(costo)
    # Es el que permitir ajustar los pesos de nuestra matriz. Es decir, si el costo = 2, ajustará los pesos
    # para que ese costo tienda a 0.
    optimizador = tf.keras.optimizers.SGD(learning_rate=0.5,momentum=0.0, nesterov=False) #.minimize(compute_loss,costo)
    print(optimizador)

    # Da el arreglo de booleanos para decirnos cuales estan bien y cuales están mal
    # argmax nos va dar el valor más alto de todas las predicciones que hizo softmax. 
    # Y se va comparar con los datos reales para decirnos si se hizo bien o mal la
    # predicción
    #prediccion = tf.equal(tf.argmax(y,1),tf.argmax(yR,1))

    # Da el % sobre el arreglo  de predicción. Si en la variable de predicción hay
    # 10 elementos, 5 están bien y 5 están mal. El % será edl 50%
    #accuracy = tf.reduce_mean(tf.cast(prediccion, tf.float32))

    #if(epoca_i%50==0):
    #    print('Epoca: {:<4} - Costo: {:<8.3} Certeza: {:<5.3}'.format(epoca_i,costo,accuracy))

for epoch in range(1):       
    ds = mnist_train.take(10)
    for image, label in tfds.as_numpy(ds):        
        avance(epoch, image, label)   

import tensorflow as tf
# Daset de datos con números escritos a manorom 
from tensorflow.examples.tutorials.mnist import input_data
# API de tensorfow para construir y entrenar modelos de alto nivel
from tensorflow import keras
from keras.utils.np_utils import to_categorical
# Librería para representación gráfica
import matplotlib.pyplot as plt
# Librería para tratar arrays
import numpy as np

# Se recuperan los datos y el metadata de los datos
#mnist_train2, mnist_info = tfds.load('mnist', split='train', as_supervised=True,  shuffle_files=True,with_info=True)
# De los datos, se extrae los datos de entrenamiento y test
mnist = tf.keras.datasets.mnist
(x_train_orig, y_train_orig), (x_test_orig, y_test_orig) = mnist.load_data()
x_train = x_train_orig.reshape(x_train.shape[0], 784)
x_test = x_test_orig.reshape(x_test.shape[0], 784)

# El formato original esta en "unit8" con lo que se tiene que convertir en un float32 para que funcione
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')

#Se divide la imagen en 255 porque es la escala de grises y es mejor operar con 0 y 1. Más sencillo
x_train, x_test = x_train / 255.0, x_test / 255.0

# Paso necesario porque devuelve los registros y toda la información en la misma columna. Pero 
# se necesita esos valores esten en un matriz de 10 columnas para calcular bien los acietros.
y_train = to_categorical(y_train_orig, 10)
y_test = to_categorical(y_test_orig, 10)

# El modelo keras se basa en capas donde vas añadiendolas para 
# ir construyendo la red neuronal
model = tf.keras.Sequential()
# La función sigmoid es la que hace el calculo de peso. Haría primero:
# 1. y = tf.matmul(x,P)+b en la versión que no funciona 
# 2. Luego devolvería 0 o 1 según se acerque al valor. Que sería, creo, calcular el gradiente
# descendiente. Es por ello que los datos de entrada se 
# dividen entre 255 para obtener un valor entre 0 y 1.
model.add(tf.keras.layers.Dense(10,activation='sigmoid', input_shape=(784,)))
# Esta función es la que se encarga de calcular la probabilidad que 
# el resultado devuelto en el paso anterior a que número pertenzca. Por eso
# la red neuronal tiene 10 columnas, y las etiquetas del set de datos
# se han convertido a 10.
model.add(tf.keras.layers.Dense(10,activation='softmax'))

# Este paso es opcional y permite ver los parámetros de cada capa que se añade
# La primera es que se usa para el calculo de pesos y la gradiente descendiente
# y tiene 7850. Que son 784 de la entrada de datos(28x28)*10(número de neuronas de entrada)
# + 10 sesgo.
# La segunda capa son 10 neuronas de salida *10 del paso anterior + 10 del sesgo
model.summary()

# Este es el paso de configuración del aprendizaje del modelo
# El parámetro "loss" es que la algoritmo/proceso de calculo en el softmax. 
# En el parámetro "optimizer" es el algoritmo que se usa para el calculo de peso y el gradiente descendiente
# El parámetro "metrics" sirve para monitorizar el proceso de entrenamiento. Hay varias metricas que se puede usar
# pero en el ejemplo solo usa esta.
model.compile(loss="categorical_crossentropy", optimizer="sgd",metrics = ['accuracy'])

# Ahora toca entrenar el modelo. Se le pasan los datos de entrenamiento y sus etiquetas
# El nuúmero de "epochs" es la veces que se va entrenar el algoritmo
# Hay un parámetro que no esta que es el batch_size que indica cuantos datos se van a usar 
# para calcular los parámetro del modelo(los pesos)
# El parámetro verbose es para indicar si nos va dar salida de los pasos que va haciendo
# 0 = no sale nada. 1 barra de progreso. 2 una linea por epoch
model.fit(x_train, y_train, epochs=10, verbose=1)

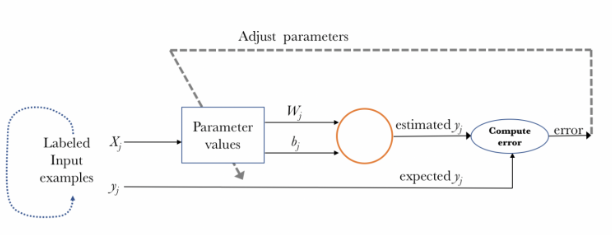
# Evaluar el modelo a partir de los datos de test.
test_loss, test_acc = model.evaluate(x_test, y_test)

# En el paso anterior devolverá el % de acierto porque al modelo le hemos indicado
# que muestre el progreso que va haciendo. Pero también se puede saber 
# mostrando el resultado de la variable
print("% de acierto", test_acc)

# Ahora vamos a predecir el número de una imagen de test.
# Numero de imagen que vamos a usar, será 5. Y la mostramos antes de nada
image = 5
# Para que se visualice hay que usarl el modelo de original sin transformar
plt.imshow(x_test_orig[image], cmap=plt.cm.binary)

# Le pasamos al modelo los datos que se usarán para la predicción. Que es el transformado
prediction = model.predict(x_test)

# el np.argmax nos dice el índice del vector que tiene la posición más alta. 
# La salida de la red es una matriz de 10 columnas. Donde en cada una de ellas contendrá 0 o 1
# según la predicción del modelo.
print("Número que se predice: ", np.argmax(prediction[image]) )